Pseudolecture 13 postponed to October 3

 Hi everyone,

I was afraid this would happen — I forgot to set my alarms last night, and just woke up, and won’t have things sufficiently ready for today’s scheduled pseudolecture. So I’ll have to postpone it.

There are still two more to go. The next one will not be next week — it will be the week after next (Saturday October 3). There is a new seminar, approximately monthly, by Dawei Chen and Qile Chen at Boston College, with two talks , and the second will conflict with AGGITOC’s regular time: https://sites.google.com/bc.edu/map/home . There will be some people interested in both events. (Next week’s second speaker is Hannah Larson, who is definitely worth catching, incidentally.)

I’ve posted this on zulip and the Algebraic Geometry Discord, so I hope this reaches everyone!

 

Fibered products: more thoughts between pseudolectures 11 and 12

Once we wrapped our heads around what morphisms of schemes are like, I jumped ahead to chapter 9 to show that fibered products exist. I did this for a few reasons. I wanted to make clear that there was nothing stopping us from immediately understanding fibered products. (The reason I left it after chapter 8 in the notes is that it can take some time to digest it the first time you see it, and there was lower-hanging fruit to pick. Also, once you begin to think about the fibered product, you are led to consider many other things, so it is a substantive topic in its own right.

What I most want you to do is to listen to my exhortations about how the existence is, understood properly, “easy” (in the technical sense — it is conceptual, although you have to train your mind in order to make it natural). So watch and read and digest. Once you have digested it, you are free to read more about Yoneda’s Lemma, and “Zariski sheaves” and Grothendieck topologies — but only if you are at the stage where these are easy reads, and not when they are entrancing but opaque.

I would then recommend trying a bunch of explicit problems in section 9.2, which we haven’t discussed yet, but will let you see that you can really work with fibered products in practice. For this, you need to know something about tensor product — but you’ll find out how little there is to actually know, and how everything follows from these few facts. Section 9.3 is just about interpreting “pullbacks” and “fibers” in terms of fibered product. (Example 9.3.4, on a double-cover of the line, is super-enlightening, and I discussed it in the last pseudolecture.) And from there you can easily see why various properties are preserved by base change/pullback/fibered product (section 9.4). (Please skip 9.5, even if it would be otherwise very interesting to you — it is in the process of being rewritten.) So at this point you can plausibly be done most of chapter 9 (except for 9.5 which I asked you to skip, and 9.6, which isn’t hard, but which I’ve not yet talked about in a pseudolecture).

Here are some problems from chapter 9 that are worth trying.

If you are new to a lot of this, you can try Exercise 9.1.A, which doesn’t build on lots of other things, so you get a chance to just understand something without having to remember a huge superstructure beneath it. 9.1.B is the key connection that gets us from algebra to geometry (the “local model” of the fibered product).

On the other hand, if you are a fancy person, you can do the exercises to understand the existence of fibered products in terms of representable sheaves.

In section 9.2, I would recommend all the exercises that are the gateways through which algebra becomes geometry: 9.2.A, 9.2.B, 9.2.F

Then you can understand how to change “base fields” in this language, to for example relate things over $\mathbb{Q}$ to things over $\overline{\mathbb{Q}}$ to thinks over $\mathbb{C}$. Exercises 9.2.H to 9.2.J deal with this.

If you are a fancy person, you can try 9.2.E, which includes a ring that Jonathan Wise mentioned a few pseudolectures ago — .

And Exercise 9.2.K is not important in any way, but it is entertaining!

In Section 9.3, 9.3.A will give you some insight into fibered products — it works well for topological spaces.

In Section 9.4, if you do a few parts of problem 9.4.B, showing that various properties of morphisms are preserved by base change, then you’ll see how to do this in general.

That’s all the time I have for today — tomorrow I’ll hopefully write down a bit about classes of morphisms of schemes. I should really have done that before telling you to do Exercise 9.4.B.

---

I am leaning more and more toward having some “office hours” on zulip, so I can actually answer some questions you may have — I might pick a time and be there, and then I would come back to it periodically, so people can ask questions asynchronously. But only if it would be useful to enough of you (at least a few)…

 

Between pseudolectures 11 and 12

As I mentioned at the start of pseudolecture 11, my intent is for this “edition” of AGITTOC to end in two or three weeks. Then I will pause for a month or so, and I might then begin a new edition, starting very roughly where we left off, but with presumably a somewhat different audience.

In this post, I’d like to go over the material we are talking about in these few pseudolectures, to give some sort of written overview, and to suggest problems to do.

Let’s resume our story at the start of part III of the notes, at the start of chapter 6. What do we mean by maps of geometric spaces, now that we have some idea of how we want to think of the geometric spaces by themselves? Certainly we will have to understand maps of points, open sets, and functions, and we will want to understand how our “local models” map. (If you are not seeing this for the first time, you may enjoy trying to do this simultaneously in several categories — varieties over an algebraically closed field; schemes; and complex analytic spaces — to really see what is essential about the constructions, and what is specific.

We are quickly led to the notion of a morphism of ringed spaces. If we are careful, we are led to the notion of a morphism of locally ringed spaces. More specifically, at the very start of our journey, we were expecting that the locus where functions vanish should be a closed subset (this came out in questions and comments on zulip and in the first couple of pseudolectures). This drove our definition of the Zariski topology, and furthermore made us realize that the stalks of our spaces were local rings (thus handing us the definition of locally ringed spaces). With locally ringed spaces, we had the notion of the value of a function at a point as well.

So all of this helps motivate how a map of locally ringed space should be correctly defined — it is a map of ringed spaces such that “the pullback of the locus where a function vanishes should be the locus where the pullback of the function vanishes” (and hence for “doesn’t vanish” as well).

So, to make friends with this, try Problem 6.2.A (morphisms of ringed spaces glue) and 6.3.A (morphisms of locally ringed spaces glue).

If you are quite new to this, try 6.2.B and 6.2.C, which might be more tractable, and are also important.

Everyone should do 6.2.D — it provides the local model of or morphism.

Question everyone has: why do we need locally ringed spaces? What’s an example of a morphism of ringed spaces that is not a morphism of locally ringed spaces? What’s a morphism as ringed spaces that doesn’t correspond to a map as rings? For this, you should do Exercise 6.2.E. We won’t really need it, but it is good to see.

Important exercise 6.3.C will show you how thinking in terms of morphisms of locally ringed spaces forces Spec’s to map the way you want them too.

Exercise 6.3.E is enlightening if you want to see how things you might already understand (about how to think about projective space) translates into our new language.

Exericse 6.3.F — that maps to an affine scheme are the same as ring maps in the opposite direction — is crucial, and a must-do — it has already been used multiple times by the time I write this.

Exercises 6.3.J and 6.3.K came up in the question period in the eleventh pseudolecture — maps from an affine scheme that is “local” are very understandable.

Section 6.4 is about projective geometry. It is worth reading, and the one exercise to do here above all else is 6.4.A, which tells you the extent to which maps of graded rings give you maps of projective schemes. The point of the exercise is to learn why the statement is not surprising.

Section 6.5 is about rational maps, which are really “mostly-defined morphisms”. First and foremost, you should understand (precisely and intuitively) what a rational map is, and why the notion makes sense. Ignore the proof of 6.5.5, which is botched. (I’ve revised it, but not yet made the updated version public.) To get a feel for why rational maps are a useful notion, I would recommend 6.5.D (which connects it to field theory), and the many examples starting with pythagorean triples in 6.5.8. You may find it interesting that diophantine questions end up oddly paralleling questions over “function fields”.

We did not discuss representable functors and group schemes (section 6.6), but if you wish, you should read it. It requires more mathematical maturity, but you know everything you need to know to read it. Similarly, section 6.7 explains how to define a very useful classical object (the Grassmannian) which generalizes projective space. It becomes cleaner and easier later with more perspective.

That’s all the time I have right now, so I will just post this. In the next couple of days, I hope to write more about things we’ve covered, notably, the affine communication lemma, various properties of morphisms, and fibered products.

I’m also intending to spend time on zulip, and in particular answer questions and discuss things. Perhaps it would be helpful to set up a zulip channel that would be “office hours” for the week, and have a chunk of time where I could answer questions?

 

Problems to think about (up to pseudolecture 9)

As promised, I want to now give you some problems to think about, mainly in Chapter 4 and Chapter 5.

But first, a quote for the topologists among us:

It was my lot to plant the harpoon of algebraic topology into the body of the whale of algebraic geometry.

— Solomon Lefschetz (A Page of Mathematical Autobiography, Bulletin of the American Mathematical Society, Volume 74, Number 5, 1968)

The end of Chapter 3

If you are happy with 3.7.C and 3.7.D, then you are happy with the theory of this section. If you can do 3.7.B and 3.7.G, then you can work with these ideas.

The structure sheaf.

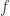Our goal here is to understand the sheaf of functions on (or ) as simply as possible. We want really to know that it is a sheaf, and to be able to work with it. The idea to keep in mind is that we will understand it only through the distinguished open subsets (where Doesn’t vanish), and will take the functions on to be 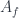, except to make sure this is well-defined (i.e, “if , then 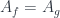“) we define the functions in a way depending only on the open set itself (Definition 4.1.1).

So Exercise 4.1.A will make sure you are completely comfortable with the second trick. And Exercise 4.1.B and Exercise 4.1.C will make sure you are comfortable with the first.

If you are already familiar with exact sequences, then Remark 4.1.4 will be a clarifying perspective.

The recurring counterexamples in 4.1.6 are good to keep in mind. You might have noticed that an example from pseudolecture 9 was a variant of the last one — 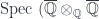is a non-Noetherian scheme for which all the stalks are Noetherian (in fact, they are fields).

Section 4.2 is all about drawing pictures. It should be fun.

In Section 4.3 there are a lot of things to get used to, so a lot of exercises worth doing. You can see if you get confused by 4.3.A. If 4.3.B is straightforward, then you’ll know you are comfortable with these ringed spacdes. 4.3.E(b) is our first (provable) example of a scheme that is not affine!

Exercise 4.3.G will finally make clear that we have defined our locally ringed space with the properties we want.

People often complain that algebraic geometry is sometimes done so “formally” that there are no examples. I agree that it is hard to really understand something without really playing with actual examples. So in 4.4, do what it takes to become comfortable with these three examples. Exercise 4.4.A is one we will use later, for example, when we defined “Proj” in pseudolecture 9. You should do 4.4.D (and then distill it to make it as painless as possible), and then you’ll really know you can compute stuff on a variety, using its cover.

Then in the next section, “Proj” is a machine to make varieties/schemes from many more open sets, but using just one ring. You may want to Exercise 4.5.B to see how homogeneous polynomials “cut out” a scheme in projective space in a hands-on way, so you’ll have a good feel for it when we think about Proj in generality.

Exercise 4.5.D will put graded rings in general into this context. Definitely do Exercise 4.5.E, and take your time with it. (Feel free to solve it in any way you want, even if it involves rearranging some of the development of the material in this section.) The following few exercises fill out the construction of Proj; try a sampling (or all of them!) to convince yourself that there is nothing tricky here. If you prefer compatible germs, do Exercise 4.5.M.

If you have seen these things before, you may want to try 4.5.Q, not because it is fancy, but because it can be confusing, and it relates to a cause of continuing confusion. Grothendieck often thinks of projectivizations of a vector space not as one-dimensional subspaces, but as one-dimensional quotients. So whenever you see “projectivize” in any algebraic geometry paper (or anything very near algebraic geometry), you have to be careful. In fact, there is method behind Grothendieck’s madness (at least this particular madness) — since he is thinking of geometric things in terms of functions on them, he is thinking of the vector space in terms of the linear functions on them (i.e., the dual vector space), and one-dimensional subspaces of a vector spaces indeed correspond to one-dimensional quotients of the dual vector space.

Okay, enough philosophizing! In chapter 5, the first section is just extending topological notions to these new things we have created. The easy exercises are important in that they make sure you can toss these notions around without thinking. I’m somewhat torn about how important 5.1.E really is — but it is worth doing!

I’d like Exercise 5.1.H to be easy, but I fear it is not. Someone should try it and let me know!

In section 5.2, the key exercise to do is Exercise 5.2.F (integral = reduced + irreducible). Exercise 5.2.H involves an important concept as well. Exercise 5.2.I is why some people start with irreducible varieties, in order to make the sheafy issues less scary.

Section 5.3 is home to the Affine Communication Lemma, which we will use repeatedly, and with great effect. You should understand the proof, and why there isn’t much there! Then the exercises give you lots of opportunities to practice with it. You should try some of the exercises involving the new notions (such as Noetherianness of schemes), but the ones I’ll most suggest you do is 5.3.H and 5.3.I.

Logically (and in pseudolecture 9), section 5.4 could come after 5.2, as it involves more “stalk-local” properties. There are some exercises to make sure you see how the theory fits together (such as 5.4.F), but the really fun ones deal with actual explicit rings (5.4.G to 5.4.L; 5.H is much more useful than it looks).

Then skip the rest of Chapter 5 (I’m in the process of completely rewriting the part on associated points and associated primes), and we will discuss morphisms of schemes in pseudolecture 10!

Plan for these problem.

You can think about these problems for the next couple of weeks. But if by next Wednesday (September 2) you can send your shepherd (or indeed any shepherd) an update on (a) what you have been working on, and (b) how it is going, that will help me figure out what to say next. Also please tell them (c) what is the most confusing thing, (d) what is the coolest thing, (e) what exercise you most want to see an answer to, and (f) what exercise you liked best.

And lastly, more inspired by the question of why the sheaf of functions is called 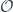, from Tomas Prochazka.

Hi Ravi,

I think you mentioned the linguistic origin of O? I read last year something about the origin of some notation in math (I don’t know to what extent is it reliable but it kind of makes sense):

O … holomorphic from Italian (where they don’t use H, not even in this word) 🙂 it’s quite funny if it is true

k … for field from German Körper (body, that’s how field is called I think in some languages, including Czech)

Z … for integers, in German Zahlen – numbers

e … for unit, again German from einheit

U,V … for open sets, German and French Umgebung (neighbourhood) and voisinage (I don’t know French)

F,G … in topology, ferme, Gebiet

finally they also said that Klein bottle was not a bottle but a surface (in German Flasche vs Fläche) but somehow there was a typo or misunderstanding and they started translating it as a bottle.

 

After pseudolecture 9

It’s been a little long since I have had a chance to do more than get the pseudolectures ready – sorry! I have just trimmed the pseudolecture videos on youtube, and added brief summaries. I intend to post trimmed versions of the slides to the pseudolectures soon.

One thing I am always struck by — the very start seems to move slowly and spend a lot of time on the “basics”, and then things seem to speed up. But that is misleading — in fact we have to get comfortable with the “essentials” at the start, and then we can move ahead quickly and with confidence.

What I would like to do next (or at least, very soon) is to get back to suggesting problems for you to think about (going back a few weeks, and also going ahead a little bit, knowing that I will have weeks where it will be difficult finding time to write). I also want to spend time on zulip.

Where we left off

At the of the previous post, we were at the end of Chapter 3, which is well behind where we are in the pseudolectures. So let’s start with Chapter 4.

The first exercise of the chapter is worth doing — checking that using our definition of the structure sheaf gives the “right answer” for distinguished open sets. Roughly speaking, on , the functions on the locus where doesn’t vanish should be the localization where you’re allowed to invert .

I wouldn’t skip understanding “base gluability” of the structure sheaf, which is the most complicated part of that argument. Reason: it’s not so bad, and it can sometimes be done in a horrible way, scarring people for life.

Exercise 4.3.A is also worth doing — it is enlightening for most, and strangely confusing (and particularly enlightening) for some — the fact that you can recover a ring from its spectrum in a precise way.

I would also try some of the “easy” exercises if you are feeling nervous — easy doesn’t mean unimportant. Exercises 4.3.F and 4.3.G are also important to know.

Section 4.4 has examples of schemes (and varieties). It is important to get your hands dirty and really get to know many examples of schemes/varieties — they aren’t abstract formalisms, but in fact an abstract way of understanding something concrete. You absolutely should understand projective space, and you may prefer the coordinates in the notes. The line with the doubled-origin is the ur-example of a “non-Hausdorff” space/variety/scheme.

We can get lots and lots of examples (and lots of important and historical examples) from projective geometry. Then in yesterday’s pseudolecture, I described the “Proj” construction. Graded rings and modules sound like they should be way more down to earth than fancy-schmancy things like schemes and strangely named rings, but in fact they can be more confusing! I think it is worth understanding in whatever way you like how to turn a graded ring into a “picture” (or more precisely, into some sort of geometric object).

Now that we know what schemes (and almost, varieties) are, we will define some adjectives which can be applied to them. You should think of these as either natural things you want names for, or else technical things that will turn out to be important, or else properties that essentially always hold in any reasonable situation (but that you need a name for). The first section has topological properties such as connected, irreducible, quasicompact. You’ll see quasiseparated there too — a horrible sounding name! But the thing to remember about quasiseparated is that it essentially always holds in reasonable situations, and it is also always accompanied by his little brother “quasicompact”. When we say a scheme is “quasicompact and quasiseparated” (sometimes abbreviated qcqs because it is so common a hypothesis), we just mean that it is built out of finitely many building blocks (i.e., covered by finitely many affine open sets), and their intersections are also built from finitely many building blocks (i.e. their intersections are themselves covered by finitely many affine open sets).

Then we have the geometric incarnations of “no nilpotents” (“no fuzz” = “reduced”) and “integral domain” (“integral”). Showing that integral = reduced + irreducible (5.2.F) is good practice.

In the pseudolecture, we next discussed two more stalk-local properties — normality and factoriality (section 5.4), and there are lots concrete examples to work out there (within hints!). You will notice that often an exercise that looks very geometric has next to it nearly the same exercise that looks very number-theoretic. There are a lot of exercises here to try to get your hands dirty. (I learned 5.4.H late in life, and have found it particularly useful for producing and understanding examples.)

Then we discussed the affine communication lemma (5.3), which is easy, powerful, and clever — it is worth reading and appreciating. Probably the people who will appreciate it the most are those who struggled with other ways of trying to make sense of well-definedness of definitions.

In particular, we are very close to defining varieties over a field — they are quasicompact reduced finite-type -schemes, that are Hausdorff. That is a strange way of saying that they aren’t built out of infinitely many pieces; they have no fuzz; they look like they are cut out by equations in (or more precisely affine $n$-space); and they are (in the correct but not literal sense) Hausdorff (which we haven’t yet defined).

You should then skip the rest of chapter 5 — I have mostly rewritten the discussion of associated points/primes because it is really quite simple when done carefully, and I am unhappy with the discussion in the earlier public version you have. I’d like to get it into a shape that I can share it with you soon, because I’d get great feedback on what works and what doesn’t work. But I know that time won’t allow it.

We’ve begun to talk about morphisms of schemes (and varieties). One of the most basic insights of Grothendieck is that we shouldn’t focus on “things” (objects in a category), but instead on “maps between things” (morphisms) — properties that seem to be about objects are in fact about morphisms (they are “relative” — they are properties of a relation = map from one object to another).

So you may be able to understand fairly quickly how morphisms of schemes can be cheaply defined using the crutch of locally ringed spaces (section 6.3). Once we do that next week, we know the category of schemes; we can now talk about lots of things. The “easy” exercises around here are a great way of solidifying and verifying your understanding.

By the end of this pseudocourse, I’d like to do a good deal of chapters 7 through 10, and conclude with a large number of examples from those chapter to give you an idea of what we can now talk about, as some consolation prize instead of proving a big punchline theorem. Although the fundamental theorem of elimination theory (and elimination of quantifiers) might qualify as a fun punchline.

That’s enough for tonight! I hope to write more soon. If you would like a more explicit list of problems to think about, just let me know (in the comments below might be easiest, but other means work well too).

 

Between pseudolectures 6 and 7

We are now at the end of Chapter 3, and the last week or so has been spent on “understanding the geometry of rings”, or “drawing rings”. In particular, you should now try to think of rings as topological spaces, and if you haven’t seen the topology on the spectrum (or “max spectrum”) of a ring (the Zariski topology) before, you should make friends with it, by thinking through examples. If you have seen it before, but don’t yet know how to draw nilpotents, then you can think about fuzzy pictures.

This coming Saturday, we’ll add in the sheaf of functions (or if you wish, the sheaf of algebraic functions, or regular functions), and at that point we will know about schemes, and can do some examples. Strangely, we won’t yet be able to define varieties, since we haven’t yet figured out how to describe the “Hausdorff condition”. But we’ll be close.

You will also be itching to know what morphisms of schemes are — that’s for the week after, if all goes well.

Here are some things to think about as you digest what we are talking about.

Things to think about.

Get comfortable with the examples of section 3.2. Even the case of the dual numbers is worthwhile.

Build your personal dictionary between algebra and geometry, and add to it as we go. I’ve been meaning to make a big one, and I keep starting, but it keeps getting big and then I misplace it.

Exercise 3.2.L is an example of how a geometric picture can tell you something algebraic that may not have been obvious.

Exercise 3.2.O is a hands-on example that will make certain you can see why ring maps correspond to set maps in the other direction. Exercise 3.2.P makes this rigorous and precise.

I mentioned Exercise 3.2.T in a pseudolecture, and it is just fun.

If you are new to many of these concepts: there are a number of specific algebra exercises (3.2.!, 3.2.B, 3.2.C, 3.2.G) that you can do.

If you have experience with differential geometry, try Exercises 3.1.A and 3.1.B. (This is worthwhile even if you don’t have much experience — you may get some practice with how to think about things.)

For those with more experience:
3.2.I(a) gives you one way (from Mumford?) of thinking of generic points. 3.2.I(b) can be pretty tricky.
Related: prove that the maximal ideals of are in some sort of “obvious” bijection with the Galois orbits of .

On the Zariski topology: there are a number of problems you should do if you haven’t seen it before. Pick problems in Section 3.4 to do. If you can, you should make them all second nature. Exercise 3.4.J has an insight that we will use repeatedly. (Exercise 3.5.E is an easy variant of it.) Exercise 3.5.B has a useful trick that comes up in ring theory a lot.

In the section on topological properties (3.6), we won’t need too much of it in depth, but it is important that you become happy with point set topology, and ideally have it digested into your unconscious. Exercise 3.6.N makes my “zen” comments about generic points somewhat more precise.

Noetherian rings turn out to be incredibly important, and it is probably a crime in several European countries that I introduced them in so little time. But there is remarkably little you need to know about them (at least to get started), and that’s what I put in the exercises in Section 3.6. It also includes statements about Noetherian modules that we won’t need (any time soon at least), but if you have seen these ideas before, you may as well make sure you’re happy with everything.

The “” map from subsets of the spectra is important, and not hard. Theorem 3.7.1 and 3.7.E are the important correspondences between closed subsets and radical ideals, and between irreducible closed subsets and prime ideals, and are worth digesting. The first of these (3.7.1) is sometimes called Hilbert’s Nullstellensatz, and it is the “scheme-theoretic” version of the “variety” version stated earlier. Weirdly, the scheme-theoretic version is much easier!

Next pseudolecture

Because I may not have a chance to put up another post soon after the next pseudolecture, let me say something about what happens next. The crucial construction we will begin with is the ring of functions (if you wish, algebraic or regular functions) on the spectrum (or max-spectrum) of a ring, which we will define by instead defining it on a base — we declare that on the open subset of where a function $latexf$ Doesn’t vanish, the functions are — basically, we allow ourselves to divide by . I intend to give a hands-on proof even though it is more laborious than a sneak fast proof if are happy with localizations being exact. But maybe I’ll give both. (If you want to impress your friends — this is a special case of “descent”, and the general fact underlying descent is actually just this sneaky second proof, if you look at it the right way.)

So we will then know the sheaf of functions on an “affine scheme” or “affine variety”.

This construction works without change to turn an -module into a sheaf of -modules (the sections over are , which is obviously an -module).

So that means we’ll have defined what an affine scheme or variety is as a ringed space — and then we immediately know what a scheme is, or a variety (minus Hausdorffness). I would like to then do the three examples of Section 4.4 in depth, because if you understand them, you are really able to do business with schemes and varieties.

Random entertaining question for experts

(This will relate to my eventual post following up on my “category theory is central and you should never take a course on it”, retracting the last part of that statement…)

We have the notion of full functors, and faithful functors. Now fully faithful functors come up a lot. And faithful functors come up a lot. When do full functors come up? I see “full” as being a concept that mainly comes up only “after” “faithful”.

(A more dangerous question: does “essential surjectivity” of a functor come up often in cases where the functor is not already known to be fully faithful? I found it entertaining to ponder why we don’t really have a notion of “essential injectivity”…)

 

Between pseudolectures 5 and 6

Today, I finished (for the most part) discussing sheaves — in particular, we discussed inverse image sheaves. We’ve talked more about the underlying set of an affine variety or scheme (mSpec and Spec). In particular, we’ve begun to flesh out a dictionary between algebra and geometry. We saw why maps of rings give maps of Spec’s (or mSpec’s, if appropriate) in the other direction.

Things to think about in the next couple of weeks

You’re undoubtedly still thinking about things from the previous week, so here are some more things to ponder. If you are relatively new to commutative algebra, and you find that you can do exercises, then declare victory — you can learn commutative algebra as you need it. It is worth thinking through the properties we need on quotient rings, localization of rings, and Noetherian rings.

Things to read this week

On top of the things you read as of last week, you should now read the final section 2.7 on sheaves, and basically all of Chapter 3. We haven’t really discussed the topology on (m)Specs (the Zariski topology), but you have already told me how it should work — sets cut out by a bunch of functions should be declared to be closed sets, and nothing else. So you can now read all of Chapter 3 (and also think through what things mean even in the case of mSpec).

Problems to think about this week and next

For everyone: please do the same three meta-problems of what was interesting, and what was challenging, and what was confusing.
You may have noticed that your answers have a big effect on what I choose to say in the pseudolectures.

If you are new to commutative algebra: There are a bunch of things in commutative algebra that are now coming up — you may be able to understand them all, by judiciously working through exercises. I hesitate to suggest any in particular — just pick several that you think are at the border of your understanding. I am hoping that a number of you will think about the same problems, and discuss them (and call in me or some shepherds if you have questions or things to talk about). For example, you might be able to learn all you need (for now) about Noetherian rings by doing a few exercises in section 3.6.

Do what you kind to understand the inverse image sheaf. For example, 2.7.B.

Exercise 3.4.E and 3.4.F will help see what nilpotents do (or more precisely don’t do) geometrically. We’ve seen that maps of rings induce maps of (m)Spec’s in the opposite direction; 3.4.H will show you that this is a continuous map, and 3.4.I will give a bit more insight. Definitely do 3.4.J.

When you read 3.5 on distinguished open subsets, definitely solve 3.5.E if you can.

Section 3.6 has a lot of words in it, but the important concepts have already happened by 3.5. 3.6.A and Remark 3.6.3 relate to Taylor’s comments on idempotents. 3.6.B and 3.6.C give examples that help you see the weirdness of Zariski topologies. 3.6.E and 3.6.F are concrete problems that might test your understanding; perhaps 3.7.G and 3.7.H too.

In section 3.7, do 3.7.E and 3.7.F.

And next Saturday, I’ll quickly review things you have read on the Zariski topology, and we will define schemes (and, almost, varieties)!

Bonus links

There were a couple of links on zulip to help make things in tikz, and I thought they were worth highlighting:

• https://tikzcd.yichuanshen.de (from Michael Klyachman) for commutative diagrams
• https://www.mathcha.io/editor (from Torgeir Aambø) which can be used to make essentially any tikz picture, not just commutative diagrams

 

Pseudolecture 5 tomorrow

Tomorrow (July 25, 2020), at 8 am Pacific, the fifth pseudolecture will take place, in the same way as the previous one(s).  If you need more instructions, just comment below, or ask on discord or zulip!  (I’m not sure if this announcement is needed, but to be safe, I’m posting it…)

And just to give this post some more interesting content, at the Algebraic Geometry Syndicate earlier this week, James Grant pointed out that

Richard E. Borcherds has posted three series of lectures regarding algebraic geometry. These are quite good, in my opinion.

I’ve dipped into them briefly (as I just saw this), and agree!  Here’s the link.

Also, Juliette Bruce had something to add as to why  is used for sheaves of functions (taken from her comments on zulip).

Some people think the symbol was chosen in honor of Oka, sometimes it is even said that reflects the French pronunciation of holomorphe. The truth is that the symbol was chosen accidentally.  In a letter to the authors from March 22, 1982, H. Cartan writes: “Je m’étais simplement inspiré d’une notation utilisée par van der Waerden dans son classique traité ‘Moderne Algebra’ (cf. par exemple §16 de la 2e édition allemande, p.52) [I was simply inspired by a notation used by van der Waerden in his classical treastise `Modern Algebra’…”

Link here.

Further digging from Keith Conrad seems to suggestion van der Waerden’s book was based on lectures by Emmy Noether, and the notation likes originates from Dedekind to use of for an order (Ordnung in German).

Link here.

 

 

Groups, groupoids, and stacks

On groups and groupoids (in the nontechnical sense)

At this point I’ve put almost everyone who wanted to be in a group (and who hasn’t just signed up) into a group, and invited everyone to zulip and discord.  If you don’t know if you are in a group, you can go to zulip, and see if you are in any of the streams for any groups.  (I may have just added you without telling you.)  Also, if you’d like to join a particular group, anyone in that group can just subscribe you to that stream — please go ahead and do that.

I’ve found that making groups, and figuring out how to put people into groups, takes far more time than I’d expected.  (In fact, of all the things in this pseudocourse, this, of all things, was the task that was most onerous — not what I was expecting.)  So from now on, if you are not in a group (e.g. if you’ve just joined, and have gotten your invitation to zulip) and you want to be, feel free to ask me, but also feel free to ask around (perhaps people you know, perhaps just describe your background in one of the groupoids) and see if one of the groups might just take you in.

Also, you can certainly be part of more than one group if that suits you.

And now may be a good time to start rationalizing groups — if you are in a group that is fairly quiet (or completely quiet), then you can jump groups, or we can even fold the group into another one.  There are no hard and fast rules here — we just want to do whatever works well, and whatever makes people feel comfortable getting into conversations.

On stacks (in the technical sense)

A number of people are interested in hearing more about stacks, and I’m definitely open to it, with a number of caveats that are predictable to the experts.  But Taylor Dupuy  mentioned some things in the Groupoid D stream on zulip that I didn’t know about, and wanted to advertise here.

First, quoting Taylor,

before diving into the technicalities of what an algebraic stack is, you should probably read DZB’s advice here: http://www.math.emory.edu/~dzb/adviceStacks.html.

(DZB = David Zureick-Brown)

Second, Taylor has actually explained a bunch of things related to stacks!

Here is a playlist on Grothendieck Topologies:

https://www.youtube.com/playlist?list=PLJmfLfPx1Oed3osC36YKSZHJbvUWUjQ2m

Here is a video on Stacks and descent data (abstract gluing data):
https://www.youtube.com/watch?v=91fJ3GTM7Dk&t=807s

Here is a videos on morphisms of Fibered Categories (you need fibered categories to talk about stacks):
https://www.youtube.com/watch?v=piS-9sz7fkI

Here is a video on Gerbes:
https://www.youtube.com/watch?v=4sv40lsj0s4&list=PLJmfLfPx1Oec9YzTuiC-huiAGPEES3YN6

Here is a video on the idea of Algebraic Stacks:
https://www.youtube.com/watch?v=9SrNfj5OE8s&list=PLJmfLfPx1Oec9YzTuiC-huiAGPEES3YN6&index=3

Here is a video on the idea behind Algebraic Spaces and Stacks (and the representability issues) [This is where things get hard IMHO):
https://www.youtube.com/watch?v=F_-lS-pn5pQ

Here is a video on representability of Morphisms:
https://www.youtube.com/watch?v=FtHHK_sLZSg

Here is a video on stackification:
https://www.youtube.com/watch?v=0c152d66FUI&list=PLJmfLfPx1Oec9YzTuiC-huiAGPEES3YN6&index=7

Here is a paper by Moerdijk which I think is the best introduction to Stacks which a lot of those videos is based on: https://arxiv.org/pdf/math/0212266.pdf (I also used Moret-Bailey, Olssen’s book (which is the best book nowadays), and the Stacks Project). I also watched people like DZB, Ravi, and Max Leiblich talk a lot as a grad student so my videos are just like me copying them poorly.

I have some other videos on band of Gerbes, but I don’t think that is really important. In fact, I don’t think much of this is really that important for the first time through. I think you should be looking at more basic examples like curves, surfaces, linear series etc. Also, before learning about algebraic stacks you should figure out what an analytic stack (orbifold is) and why they matter. (IMHO: I think you should wait until you actually need something before you start to learn it, otherwise you run the risk of drowning in papers you don’t understand—that is what happens to me at least. Also, I forget it if I don’t use it!). Don’t worry… trouble will find you… you don’t need to go looking for it.

Not surprisingly, I agree with his point of view.  (Not surprisingly, I wanted Taylor and DZB to be shepherds….)

Something else from Taylor in Groupoid D, at nearly the same time, that I want to remember:

Commutative algebra is where the hard parts of algebraic geometry go to hide.

– Christelle Vincent

Thought of the day

While watching Abi Ward’s successful Ph.D. defense today (congratulations Abi!), I had an epiphany.  There are a few adjectives to the noun “functor” — full, faithful, essentially surjective, equivalence.  I now realize these different-sounding names are hiding their sameness.  In retrospect, essential surjective should be 0-surjective, full should be 1-surjective, and faithful should be 2-surjective.  And equivalence = 0-surjective  + 1-surjective + 2-surjective.  Then “generalizing downwards”, if you have a map of sets, then a surjective map of sets could be called “0-surjective”, and an injective map of sets would be “1-surjective”, and “0-surjective + 1-surjective = bijective.”.    In between, if you have a morphism in a category, 0-surjective would be “epimorphism”, and 1-surjective would be “monomorphism”, and 0-surjective + 1-surjectve would be “isomorphism”.

I should explain why this is true.  Certainly I am happy that I knew all of these different words before I’d try to understand them in terms of very few words.  (Similarly in a category, we could replace “object” by “0-morphism”, “morphism in a category”  or “functor between categories” by “1-morphism”, and “natural transformation of functors” by “2-morphism”…  then we could do away with almost all of these words, and just have numbers, “surjective” and “morphism”.  But then our heads would explode.

 

After the fourth pseudolecture

In the pseudolecture, I discussed more on “geometric spaces”, and at this point we have a pretty good idea of what we want if we want to make sense of something as a geometric space. We talked more about sheaves (in particular, compatible stalks, sheafification, sheaves on a base, and why using stalks we can see that sheaves of abelian groups on a given topological space form an abelian category), and we began to play around with the “local models” of the spaces we’ll discuss more (affine varieties of various sorts; and affine schemes).

Things to think about in the next couple of weeks

Make friends with some mSpec’s and Spec’s. This means go into their villages, and meet a number of them, and maybe stay over for dinner.

If you are thinking about complex analytic varieties — at this point have you fully figured out the category of complex analytic varieties?

If you are seeing sheaves on a base of a topology for the first time, can you think through why this believably has the same information as a normal kind of sheaf? If you are seeing them for the second time, I have to ask: what kind of “base” are you using? If the “usual” kind, then what does your “identity on a base” axiom look like? (Don’t look it up — I’m not asking you what’s written down by someone else!) If you are learning to think categorically (and want to — this should be done on the second pass), do you see the filtered index category lurking here?

Things to read this week

This coming week, you should be getting comfortable with everything up to the first three sections of Chapter 3, except for the last section of Chapter 1, and the last section of Chapter 2.

Problems to think about this week and next

(If the problems for different groups of people are not well-calibrated, let me know, and I’ll try to aim them better.)

For everyone: please do the same three meta-problems of what was interesting, and what was challenging, and what was confusing.

If you are new to commutative algebra:
Exercise 2.2.J might give you some practice with modules over rings. Try 2.3.C if you haven’t already. Get somewhat happy with why we can understand things about sheaves in terms of stalks, by picking a do-able problem or two in Section 2.4. Understand examples in Section 3.3 as much as you can, and practice “drawing pictures of rings”.

If you came in happy with commutative algebra:
Do 2.3.C if you haven’t already. Understand “sheaves via stalks” and “sheaves on a base” well by picking an interesting problem in each of those sections (2.4 and 2.5). Understand the examples of Section 3.3 as completely as possible.

If you are complex analytically minded:
Have you fully figured out how to think about complex analytic varieties (including morphisms between them) in the language we are using? Do you see why the fibered product of complex analytic varieties exists, for example?

If you’ve seen some commutative algebra to think about it:
Can you answer the second question I posed before the start (with rigorous proof!)? Can you describe how the maximal ideals of the polynomial ring in variables over a field should be identified with the Galois-orbits of -tuples of elements of the algebraic closure of ?

If you have already become comfortable with the ideas we are talking about:
(This is only for those who have already seen the above, because otherwise I fear you will become a lotus-eater.) Try to mix Yoneda with “maps to a space form a sheaf”. Do this without looking up the definition of a Grothendieck topology — you should try to do this (even if you fail) without being told what to do.

Here is a precise case to think through. Suppose is the category of balls (or if you prefer, polydiscs) in (where is not specified), where morphisms are holomorphic maps. Let the “functor category” of be defined by taking the objects as contravariant functors from to the category of (Sets), and morphisms are “natural transformations of functors”, so we have a (covariant!) functor , given by . Two big things:

(1)(Yoneda) Yoneda’s Lemma says that this is a faithful functor, which is why we call $Yo$ the “Yoneda embedding” of $\mathcal{G}$ into its functor category .

(2) (maps glue) Second, is a sheaf on any (considered as a topological space).

Now sits in a bigger category, the category of complex manifolds. Show that a complex manifold (not necessarily a ball!) gives an element of , and it still satisfies “Yoneda’s Lemma for ” (i.e., this element of the functor category determines up to unique isomorphism of manifolds), and also is a sheaf for all .

So: figure out what it should mean for an element of to be “a sheaf” on all elements , and see what information you need to make this make sense. (Hint: you need to know when a bunch of open embeddings into some “cover” .) You are basically going to invent an approximation of the notion of a topology on this category (otherwise known, roughly, as a Grothendieck topology).