Fun example from Nikolas Kuhn: simplest (?) example of an affine open subset of an affine scheme that is not a principal/distinguished open subset

A standard and very reasonable question people have when first learning about schemes is the following: is it true that every affine open subset of an affine scheme is a distinguished/principal open subset? The answer is (as most of you know) is “no”, so the follow-up question is: “what is a simple example that is rigorously provable to someone at the stage where they ask this question”.

Nikolas Kuhn gave a slick answer to this question. Consider the cuspidal curve $y^2=x^3$ in the plane $\mathbf{A}^2_k$ (where $k$ is of course a field), which has normalization $\mathbf{A}^1_k = \text{Spec} \; k[t]$ . Then if you remove $(1,1)$ , you get an affine open subset (why?), but that set is not even set-theoretically cut out by a single equation (hint: pull the equation back to be a function of $t$ , but notice that this equation doesn’t lie in the subring $k[x,y]/(y^2-x^3) = k[t^2, t^3] \subset k[t]$ .

Entertaining follow-up question: this affine open set is $\text{Spec} \; B$ for some ring $B$ . What is $B$ ?

Peter McNamara Says:

November 25, 2020 at 10:32 pm

Nice example! Maybe you or Nikolas can add it to the mathoverflow question about this.

Of course the hard part is to show that this scheme is actually affine. I’m hoping there’s a simple answer, maybe using only the criterion in Hartshorne Ex II.2.17(b), rather than hitting it with the hammer of tag 01YQ (a finite surjective morphism from an affine source to a Noetherian target implies the target is affine).

ravivakil Says:

November 28, 2020 at 8:50 am
Thanks Peter! I will suggest that Nikolas add it, and if he doesn’t, I will.

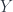About showing affineness — there is a fast way given “usual facts”, although this “usual fact” is surprisingly hard: the notion of “affine morphism” is local on the target. That means that if you have an open embedding $\pi: X \hookrightarrow Y$ , and affine-locally on $Y$ , it is “take principal open set” (hence affine), then 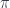$\pi$ is affine. (So if 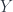$Y$ is affine, then $X$ is affine too!)

So in this case, because you are removing something locally cut out by one equation, the source is affine.

I agree that the hammer of 01YQ is too big! I don’t have Hartshorne with me right now, but I’m guessing that II.2.17(b) is the property of affine morphisms I mentioned above.

In my notes, I am changing the road by which I lead to this result. Quasicoherent sheaves are quickly and easily defined once we have the Affine Communication Lemma — the key issue is showing that “quasicoherence of an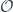 $\mathcal{O}$ -module” is affine-local. Then an affine morphism is also quickly seen to be the “same” as a quasicoherent sheaf of algebras. Then affine-locality of affine morphisms is free. (This also makes closed embeddings simpler to get to — they are just affine morphisms, where the quasicoherent sheaf of algebras is a quotient of the structure sheaf.)

But it remains an interesting question to see what the ring of this affine variety is. I’ll give you the answer, without any proof or explanation. (Level 1 question: verify that this is isomorphic to that open subvariety. Level 2: how would you discover this?)

$k[x,y,u] / (y^2-x^3, u(y-1)-(x^2+x+1), u(x-1)-(y+1))$

Nikolas Kuhn Says:

November 28, 2020 at 12:53 pm
Thanks!
I just posted the answer on MO: https://mathoverflow.net/a/377672/112142

Nikolas Kuhn Says:

November 28, 2020 at 11:43 am

Hi Ravi,
a small but important remark:You need to assume that $k$ has characteristic zero, otherwise the statement is false.

Here is a relatively easy way to check that the scheme is affine: Write down what the coordinate ring should be, and then check that the induced map is in fact an open embedding (by covering the image with distinguished affines).
Coming up with the right coordinate ring needs some geometric intuition, but this way you’ll get a fully rigorous proof, without using much at all.

ravivakil Says:

November 28, 2020 at 12:47 pm
Yes, good point about the characteristic!

Math 216: Foundations of Algebraic Geometry