(The notes for this course are here. A short url for this page is tinyurl.com/FOAG1112.)
In these days the angel of topology and the devil of abstract algebra fight for the soul of every individual discipline of mathematics.
— Hermann Weyl, 1939
There are several types of courses that can go under the name of “introduction to algebraic geometry”: complex geometry; the theory of varieties; a non-rigorous examples-based course; algebraic geometry for number theorists (perhaps focusing on elliptic curves); and more. There is a place for each of these courses. This course will deal with schemes, and will attempt to be faster and more complete and rigorous than most, but with enough examples and calculations to help develop intuition for the machinery. Such a course is normally a “second course” in algebraic geometry, and in an ideal world, people would learn this material over many years. We do not live in an ideal world. To make things worse, I am experimenting with the material, and trying to see if a non-traditional presentation will make it possible to help people learn this material better, so this year’s course is only an approximation. (See here for an earlier version.)
This course is for mathematicians intending to get near the boundary of current research, in algebraic geometry or a related part of mathematics. It is not intended for undergraduates or people in other fields; for that, people should take Brian Conrad’s undergraduate class in winter 2012, or else wait for a later incarnation of Math 216 (which will vary in style over the years).
In short, this not a course to take casually. But if you have the interest and time and energy, I will do my best to make this rewarding.
Email list: Those who filled out the sign-up sheet or told me that they wanted to be on it are now on an email list, that I’ll use occasionally, to let you know about things like changed class times and problem set corrections. If you are on the list and want to be off it, or vice versa, please let me know.
Time and place (spring quarter): 9:00-10:15 in 383-N on many Mondays, Wednesdays, and Fridays (see below for more).
Office hours: Because of the nature of this class, I’d like to be as open as possible about office hours, and not have them restricted to a few hours per week. So if you would like to chat, please let me know, and I’ll be most likely happy to meet on a couple of days’ notice. I am almost always available to meet immediately after class. If people are shy about chatting, I may turn the third “class period” each week into office hours.
References:
- The notes based on earlier versions of this class, and on many useful comments from people around the world, are available here. They will be updated throughout the year. I would very much like comments, suggestions, and corrections.
- Johan de Jong’s stacks project has in my mind become essentially the universal reference for algebraic geometry, and becoming more so with every edit. It is free, comprehensive, well-written, philosophically well thought through, searchable, and (important for a reference) modular (when you look something up, you can read “around it” to understand the proof).
- Other more “text-like” references: It may be useful having Hartshorne’s Algebraic Geometry, and possibly Mumford’s Red Book of Varieties and Schemes (the first edition is better, as Springer introduced errors into the second edition by retyping it). Mumford’s second edition is available online (with a Stanford account) from Springer.
- For background on commutative algebra, I’d suggest consulting Eisenbud’s Commutative Algebra with a View toward Algebraic Geometry or Atiyah and MacDonald’s Commutative Algebra.
- For background on abstract nonsense, Weibel’s Introduction to Homological Algebra is good to have handy. Freyd’s Abelian Categories is available online (free and legally) here.
Homework:
You can wave your hands all you want, but it still won’t make you fly.
— Mark Kisin
Unlike most advanced graduate courses, there will be homework. It is important — this material is very dense, and the only way to understand it is to grapple with it at close range. There will be a problem set most weeks. Your grade will depend on the problem sets.
Fall quarter
Monday, September 26: 2.1-2.3.7. Welcome; what is algebraic geometry?; about the course; why you shouldn’t take this course; categories, universal properties, localization, tensor product.
Wednesday, September 28: office hours. This is a test to see if having a set time for office hours (as opposed to meeting by appointment) is useful for people.
Friday, September 30: 2.3.8-2.6. Yoneda, (co)limits, adjoints, abelian categories. Problem set 1 out (based on Sept. 5 version of the notes; due Fri. Oct. 7; updated Wed. Oct. 5, but not important enough a change to announce by email).
Monday, October 3: office hours (and discussion of categories for those wanting more time with them).
Wednesday, October 5: 3.1-3.4.F. (Pre)sheaves: example, definitions, section, restriction map, stalk, germ, identity, gluability, skyscraper, constant (pre)sheaf, pushforward, ringed space, O-module, morphisms of (pre)sheaves, sheaf Hom, presheaves form an abelian category, properties determined at the level of stalks.
Revised notes posted at the usual place. (The change most likely to confuse you: the old exercise 3.4.C was a repeat and is removed, so the lettering of exercises in 3.4 has changed.)
Friday, October 7: rest of chapter 3. Sheafification, sheaves of abelian groups (and O_X-modules) form an abelian category for “easy” reasons; sheaves on a base of a topology; inverse image sheaf. Problem set 1 due. Problem set 2 out (based on the Oct. 5 version of the notes; due Fri. Oct. 14).
Most of you have seen Spec A (and its Zariski topology), so any of you who don’t should brush up on that before next class.
Wednesday, October 12: 4.1-4.5, the topological space Spec A.
Friday, October 14: 4.6 – Theorem 5.1.2. Topological and Noetherian conditions; I(.); the structure sheaf on the distinguished base of Spec A. Problem set 2 due. Problem set 3 out (based on the Oct. 5 version of the notes; due Fri. Oct. 21).
Caution: I will soon reorganize 4.6 to present the topological notions in a better order. This will result in the problems in this section being renamed.
Wednesday, October 19: 5.1-5.4.3. Definition of schemes, and first examples.
Friday, October 21: the rest of chapter 5. Examples of schemes, including the Proj construction. Problem set 3 due. Problem set 4 out (based on the Oct. 21 version of the notes; due Fri. Oct. 28).
Wednesday, October 26: 6.1-6.3. Properties of schemes: topological (including quasiseparatedness), reducedness and integrality, and affine-local properties (Noetherian schemes, finite type A-schemes, …).
Friday, October 28: 6.4, 7.1-7.2. Normality and factoriality. Philosophy about morphisms of schemes and ringed spaces. Problem set 4 due. Problem set 5 out (based on the Oct. 21 version of the notes; due Fri. Nov. 4).
Wednesday, November 2: 6.5, 7.3. Associated points (Emerton-ized version); morphisms of locally ringed spaces and schemes.
Friday, November 4: 7.3-7.5. Problem set 5 due. Problem set 6 out (based on the Oct. 30 version of the notes; unimportant typos fixed Nov. 5; due Fri. Nov. 11).
We won’t do 7.6 or 7.7 in class unless people vote to do so. But I’m happy to discuss it at length with anyone interested.
Wednesday, November 9: 8.1-8.3. Algebraic facts: integral homomorphism/extension, lying over and going-up, Nakayama. Good properties of morphisms: open immersion, quasicompact, quasiseparated, affine, finite, integral, (locally) finite type, quasifinite, and possibly (locally) finite presentation.
Friday, November 11: 8.4. Images of morphisms: Chevalley’s Theorem and the Fundamental Theorem of Elimination Theory. (Bold claim: the FTET is one of the top 10 theorems of the 19th century.) Problem set 6 due. Problem set 7 out (based on the Oct. 30 version of the notes; due Fri. Nov. 18).
Wednesday, November 16: 9.1, 9.2. Closed subschemes (and criterion in terms of affines). Locally closed embeddings/immersions. Fun projective geometry.
Friday, November 18: 9.3, 8.1. Key fact: scheme-theoretic image of (is well-behaved if
is quasicompact or
is reduced). Scheme-theoretic closure, reduced subscheme structure on a closed subset, reduction of a scheme. Fibered products exist (and generalities on deep things going on behind the proof). Problem set 7 due. Problem set 8 out (based on the Oct. 30 version of the notes; due Fri. Dec. 2).
Wednesday, November 30: 10.2-10.5. Examples of fibered products (explicit computations; Segre embedding). Interpretation as pullback (including fibers). Properties preserved by base change.
Friday, December 2. 10.6-11.1. Normalization (including in a function field extension), (quasi)separatedness, and the cancellation theorem for properties of morphisms. Problem Set 8 due. Problem set 9 out (based on the Dec. 3 version of the notes; due Fri. Dec. 9).
Wednesday, December 7: 11.2-12.1. The reduced-to-separated theorem, and related ideas; proper morphisms; introduction to dimension and codimension.
Friday, December 9: 12.2. Dimension = transcendence degree for varieties. Extended concluding example: lines on surfaces in P^3. Problem Set 9 due.
Thursday, December 22: Problem set 10 out (based on the Dec. 20 version of the notes; due Fri. Jan. 13).
Winter quarter
Most classes will be on Wednesdays and Fridays, but some will be on Mondays.
Wednesday, January 11: 12.3. Hard facts in codimension 1 (Krull and Hartogs). Intuition for behavior of dimension of fibers. 12.3.
Friday, January 13: 12.4. dimensions of fibers of morphisms. (Caution: The Jan. 14 version of 12.4 is not yet sufficiently edited.) Problem set 11 out (based on the Jan. 14 version of the notes; due Fri. Jan. 20).
Wednesday, January 18: 13.1-2. Zariski (co)tangent space, nonsingularity, smoothness over a field.
Friday, January 20: 13.3-4. Nice but inessential facts about regular local rings; discrete valuation rings.
Monday, January 30: Problem set 11 due.
Wednesday, February 1: 13.5, 14.1. Valuative criteria. Vector bundles and locally free sheaves.
Friday, February 3: 14.2-14.6. Quasicoherent sheaves and how to think of them in terms of modules over rings; characterization by distinguished inclusions of affines; module-like constructions; finiteness conditions on modules.
Monday, February 6: 14.6, 14.7, 15.1: finite type and coherent sheaves, and the ways in which they are like (and not like) finite rank vector bundles; the line bundles O(n) on projective space.
Wednesday, February 8: 15.2: line bundles and Weil divisors. This is a much trickier topic than it seems!
Friday, February 10: chapter 16. Quasicoherent sheaves on projective A-schemes. O(n) on Proj; (finitely) globally generated (at a point); base points/locus, base-point-free, linear series; Serre’s Theorem A (to be proved later).
Monday, February 13: 17.1-3. Pullbacks of quasicoherent sheaves: three (sort-of) constructions (with much help from Daniel Litt).
Wednesday, February 15: 17.3-17.5. Properties and applications of pullback of quasicoherent sheaves; line bundles and maps to projective schemes; the curve-to-projective extension theorem.
Friday, February 17: 17.6. Very ample and ample line bundles (over a ring). We spent most of our time proving the equivalence of five definitions of ampleness (which includes Serre’s Theorem A), and this probably required more sustained effort than anything we’ve done so far. The essential things to remember: know the statements of (a), (a’), and (b), and do (or at least) read the important exercises.
Monday, February 20: 18.1, 20.1. Relative Spec. Brief discussion of relative Proj (I “sort of” defined projective morphism, but left it for a later day.) Desired properties of cohomology, and applications thereof.
Friday, February 24: 20.2. Construction of Cech cohomology (of quasicoherent sheaves on quasicompact separated A-schemes), and properties. Problem set 12 out (based on the Feb. 24 version of the notes; due Mon. March 5).
Wednesday, February 28: Problem set 13 out (based on the Feb. 25 version of the notes; due Fri. March 9).
Monday, March 5: 18.2-18.4. Relative Proj, projective morphisms, and applications to curves. Problem set 12 due.
Wednesday, March 7: 20.3-20.4. Cohomology of line bundles on projective space. Applications: Riemann-Roch, degree of coherent sheaves on a curve, …
Friday, March 9: 20.4-20.5. Serre duality (statement of one version), Hilbert polynomials and functions, genus. Problem set 13 due. Problem set 14 out (based on the Mar. 5 version of the notes; due Fri. March 16).
Monday, March 12: 20.6-21.1. Serre’s cohomological criterion for ampleness, Grothendieck’s coherence theorem, Chow’s lemma (proofs left to notes, as we won’t use them much). Higher pushforwards, and their properties. A criterion for a morphism to be a closed embedding.
Wednesday, March 14: 21.2-4. Crucial generalities about curves; curves of genus 0; hyperelliptic curves.
Friday, March 16: 21.5-21.8.9: curves of genus 2, 3, and 1. Problem set 14 due.
Spring Quarter
We will now meet in 383-N.
Monday, April 2: 21.4 (new section), 21.10-21.11. Pappus’s Theorem and Pascal’s Theorem. Elliptic curves are group varieties. Fun counterexamples involving elliptic curves.
Wednesday, April 4: 22.1-2. Intersection products, and intersection theory on a surface. Problem set 15 out (based on the April 4 version of the notes; due Fri. April 13).
Monday, April 9: 22.3, 20.4.9, 22.4. The Grothendieck group of coherent sheaves; numerical equivalence; -line bundles and
; the nef and ample cones; Nakai’s criterion for ampleness.
Wednesday, April 11: 22.4, 23.1, 23.2. Kleiman’s criterion for ampleness. Differentials: motivation, definition (in the affine case), and first properties. The relative cotangent and conormal sequences, and the conormal sheaf.
Monday, April 16: 23.2-3: more differentials; examples. Problem set 16 out (based on the April 13 version of the notes; due Fri. April 27).
Monday, April 23: 23.3-4: the Euler exact sequence; using the (co)tangent bundle to understand smooth varieties.
Wednesday, April 25: 23.5-24.4: Riemann-Hurwitz; derived functors and spectral sequences; derived functor cohomology of O-modules.
Monday, April 30: 24.5, 25.1: Cech cohomology = derived functor cohomology (with the key step a clever argument of Martin Olsson); some advance perspective on flatness.
Wednesday, May 2: 25.2-4: easier flatness facts; flatness through Tor (cohomological interpretation of flatness); ideal-theoretic criteria for flatness. Problem set 17 out (based on the May 2 version of the notes; due Fri. May 11).
Friday, May 4: 25.5-6. Topological aspects of flatness: faithful flatness, going down for flat morphisms, openness, fiber dimension, flatness of relative dimension n, generic flatness. Local criteria for flatness, statements of the local slicing criterion and fibral flatness.
Monday, May 7: 25.6.4-25.8.5. Proof of the local slicing criterion for flatness. Flatness implies constant Euler characteristic (with seemingly no Noetherian hypotheses), and consequences. Philosophy and statements of the Semicontinuity Theorem, Grauert’s Theorem, and the Cohomology and Base Change Theorem.
Wednesday, May 9: 25.8-9. Cohomology and base change theorems: applications and proof.
Wednesday, May 16: 25.9-10, 7.7, 17.7. Moduli spaces: the Hilbert scheme (facts, no proof); the Grassmannian; degree d hypersurfaces are parametrized by a projective space. Problem set 18 out (based on the May 16 version of the notes; due Fri. May 25).
Friday, May 18: 30.1-30.4.2. Serre duality in various forms. Property of Ext and sheaf-Ext. Proof of “strong Serre duality” for projective space.
Monday, May 21: 30. Serre duality continued. A better world (?) of working with complexes, and the derived category (Ext^a(A,B) x Ext^b(B,C) –> Ext^{a+b}(A,C)); j^! for closed embeddings j (a right-adjoint to the exact functor j_*, which thus takes injectives to injectives).
Wednesday, May 23: 30. Proof of various forms of Serre duality.
Wednesday, May 30: 30, 26. The adjunction formula for the dualizing sheaf. For smooth varieties, the algebraic volume form is dualizing. Smooth, etale, unramified morphisms: definitions and first properties.
Friday, June 1: 26. Harder properties of smooth (and etale) morphisms. Generic smoothness and the Kleiman-Bertini theorem. (And one last patch/simplification to our proof of Serre duality!)
Monday, June 4: 26, 29.1-3. Bertini’s theorem and applications. The 27 lines on a smooth cubic surface (part 1).
Wednesday, June 6: 29.3-4. The 27 lines on a cubic surface (part 2).
—



October 6, 2011 at 9:00 am
[…] 2011-12 course […]
October 30, 2011 at 3:29 pm
[…] 2011-12 course […]
December 21, 2011 at 12:50 pm
[…] 2011-12 course […]
February 13, 2012 at 7:02 pm
What are the best Stanford math classes?…
I have not taken this class, but Ravi Vakil’s Algebraic Geometry (Math 216) class seems like a gem. His blog [0] and the notes [1] from the class are amazing. Outside of Griffiths and Harris, his class notes were my main source of Algebraic Geometry k…
February 28, 2012 at 11:35 am
In case people are just watching for changes in the comments: A revised version was posted today (Feb. 25) in the usual place. Things are quite tidy up to 17.3. The sections on Weil divisors and line bundles (15.2), global generation and base-point-freeness (16.3), and pullbacks of quasicoherent sheaves (17.3) are the trickiest parts in the latest round of edits, that I’ve tried to make less tricky.
March 26, 2012 at 9:12 pm
[…] 2011-12 course […]
April 13, 2013 at 11:04 am
I was just re-reading the section on spectral sequences (which, incidentally, is a spectacular introduction to a traditionally intimidating topic) and found that the earlier notation of and
and  in superscripts and subscripts had been replaced by a notation of
in superscripts and subscripts had been replaced by a notation of  and
and 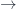 . Personally, I found the earlier notation much easier to follow; the new symbols, for whatever reason, require more conscious effort for me to parse as subscripts and superscripts.
. Personally, I found the earlier notation much easier to follow; the new symbols, for whatever reason, require more conscious effort for me to parse as subscripts and superscripts.
April 14, 2013 at 4:33 am
Thanks Charles! Does anyone else have an opinion? I made the change for precisely the same (or precisely the opposite) reason: I thought that people wouldn’t realize that the and
and  were intended to signify directions, and would be more confusing. I’d like to go with the general sense of the intended audience, so I’ll asking this year’s reading group at Stanford, and also see if any of you (beside Charles) express an opinion.
were intended to signify directions, and would be more confusing. I’d like to go with the general sense of the intended audience, so I’ll asking this year’s reading group at Stanford, and also see if any of you (beside Charles) express an opinion.
I like Charles’ taste and thoughtfulness on things like this, so I take this seriously.