The twelfth post is the March 10 version in the usual place. This post covers up to 20.3 (although more is included). The next post should appear on April 2. Corrections from numerous people, including Darij Greenberg (in the spectral sequences section) and Jason Ferguson (in chapters up to 3, with more changes still to be made). I continue to be way way behind on responding to comments, including a number from the fall (!).
This installment includes chapter 18, on relative Spec and Proj, and projective morphisms; the double-starred chapter 19, on blowing-up; and chapter 20, on Cech cohomology.
I’ve not looked over Chapter 19 in a very long time, so look at it at your own risk. (But comments are still welcome of course!) Update: it has now been edited, see this March 16 post.
I am somewhat surprised to find that there isn’t much to go: we’re through most of the notes. If you look at the table of contents, you’ll see that there are about 100 pages of the current rough draft still to come. There are one of two more chapters still to be written (one on the “formal functions” theorem and consequences, and very possibly one one Cohen-Macaulayness). So we’re almost there! (Of course, there are lots of things that need revisiting, and lots of comments still to respond to.)
For learners.
Read Chapter 18, and 20.1-20.3. (The reading next time will start with 20.4.)
18.1 gives the relative version of Spec, and re-interprets affine morphisms. It is pleasant.
On the other hand, 18.2 gives the relative version of Proj, and like Proj, it is less pleasant. I am not sure if I’m giving the “right” definition, and will ask the experts below. Any suggestions on how to make this better would be appreciated.
As a result of the weirdness of Proj, the notion of projective morphisms (18.3) is surprisingly tricky. But it isn’t so terrible. Notice in particular that finite morphisms are projective.
In 18.4, we see some of these ideas in action, applied to curves. (We’ll soon be talking about curves at great length, likely in the 13th notes.)
Skip Chapter 19 (unless you really don’t want to). It deals with blow-ups, which we won’t use a huge amount.
Chapter 20 is about Cech cohomology. Cohomology is lots of fun, and for me the highlight of the course. It is surprisingly simple (certainly compared to what you have done so far). It is amazing what you can do with it right away; we’ll start exploring that in 20.4 (and 20.5 and 20.6), and when we look at curves in Chapter 21. In 20.1, we first discuss what we want cohomology to do for us.
In 20.2 we actually define it, and verify that these key properties hold.
In 20.3, we do a key computation, of the cohomology of line bundles in projective space.
And then you are set to do some fun applications, which we’ll get into next time. But if you want to read ahead, the rest of Chapter 20 is included.
Here is a selection of interesting and/or important problems: 18.1.A, 18.1.B, 18.1.F, 18.2.A, 18.2.C, 18.2.F, 18.2.G, 18.3.C, 18.3.E (surprisingly but pleasantly intricate), 18.3.G, 18.3.H, 18.4.E, 20.1.B, 20.1.D, 20.2.C, 20.2.D, 20.2.G. As always, I hope you try more.
Here are some problems dealing with explicit examples: 18.1.H, 18.4.D (especially for number theorists), 20.2.A, 20.3.A, 20.3.B. And many more examples are coming up in 20.4 onwards!
If you solve 20.2.E, please let me know; it seems surprisingly tricky. (But people have solved it, for example Nick Haber, Mike Lipnowski, and I think Jeremy Miller.)
For experts.
18.2: I feel like I go through contortions in defining SheafProj. The right universal property would make this better. Do you have expositions you prefer?
18.3 on projective morphisms: there are multiple definitions of projective morphism in the literature, which are not all the same. The Stacks Project (as usual) does a good job of sorting this out. I stick with EGA’s definition (rather than Hartshorne’s): I really want all finite morphisms to be projective! (I wish O(1) were part of the definition. I don’t like saying “there exists a very ample line bundle” because I don’t like using the weasel phrase “there exists” in a definition, as it is less well behaved than if one makes a choice.) The fact that composition of projective morphisms are projective I only manage to prove if the target is quasicompact. (Is there an easy counterexample otherwise?)
(Aside: I remember when learning the subject being confused for some time as to why a map from one projective curve to another is necessarily projective.)
About cohomology: I’m continually surprised and delighted by how beautiful this subject is. I had been led to think otherwise when first learning it.
An inflammatory comment (that I’ve made enough times that some people are sick of hearing it): cohomology in algebraic geometry seems to be traditionally introduced through derived functors. I remain unconvinced that this is a good way to introduce it to someone learning the subject for the first time (from a typical background — I’d make exceptions from people who had worked with homological algebra a fair bit before). In particular, it makes the subject misleadingly hard, in that you need more work to get to the basic results (i.e. building up the machinery of derived functors). There is little in Hartshorne, for example, that isn’t more easily done with Cech cohomology. (An explicit list: the Leray spectral sequence seems easier to prove in this way. And Serre duality can’t really be discussed without it, because you need derived functors to even define Ext.) Don’t get me wrong: I realize derived functors are important. But I find that they naturally come second, after the learner has had fun with explicit examples.
For everyone
The description of the cohomology of line bundles on projective space was inspired by Daniel Erman’s explanation of the proof given in Miller and Sturmfels’ excellent book “Combinatorial Commutative Algebra”.
March 12, 2011 at 6:59 am
Ravi, it seems to me that the first method proposed for blow-up constructions in your notes is invalid. The basic problem is that blow-ups do not commute with non-flat base change (in terms of homogeneous coordinate ring, tensoring up an ideal sheaf may not yield an ideal sheaf; in terms of the universal property, non-zerodivisors may not pull back to such under a non-flat map). This is related to a delicate feature of the universal property of blow-up that I think you should stress in the notes: although we can characterize Bl_Y(X) as being final among a special class of X-schemes (namely, those for which the pullback of Y is Cartier), it is definitely not characterized by any nice property among *all* X-schemes.
That is, plenty of X-schemes factor through the blow-up without having that Cartier property, and there’s not much we can say about such cases (e.g., their factorization through the blow-up is not unique). This is the real reason that your first proposed method for blow-ups is wrong. In more concrete terms, for general {f_1,…,f_n} in B, there will be zillions of relations among the f’s that do not arise from relations among {x_1,….,x_n} in Z[x_1,….,x_n].
Think about the simplest possible example: blowing up a locally principal ideal that is not necessarily Cartier. We have B and an element f in B, and wish to blow up Spec(B) along Spec(B/(f)). This blow-up is again affine, in fact it is Spec(B/J) where J is the ideal of elements killed by a power of f. There’s no way we could ever compute that ideal by a calculation with a finite type polynomial ring over Z (let alone using blow-up of origin in A^1_Z, which is itself!). Likewise, in general when dealing with non-noetherian schemes and finitely generated q-coherent ideals, there’s no reason the blow-up should be finitely presented, so it cannot be obtained via pullback of a construction of finite type over Z.
I found these kinds of things to be very disorienting when I first figured out what was going on with blow-ups, and it is the reason that in my paper on Nagata compactifications (which I largely wrote when I was in graduate school) I inserted more explanation than Deligne gave when discussing “review of blow-ups” in the first section. Personally, I find the most instructive construction of blow-ups to be neither of the two methods in the notes, but the one I learned from Deligne’s note on Nagata compactifications: by giving a functorial meaning to various open affines which we glue together via universal properties (and prove a-posteriori to give the Proj definition). This is in the spirit of the functorial meaning of the affine charts and gluing among them in the definition/construction of P^n. It also has the advantage of making computations readily accessible (provided of course one can eyeball “all the relations”, feasible in concrete examples).
March 14, 2011 at 4:25 pm
Ravi, I now see that I overlooked your back-reference to 19.2.7. OK, so it all looks good, mea culpa. Nonetheless, I’d still like to advocate for the direct construction by killing f_i-power torsion on the various pieces. This has the virtue of working in analytic settings (over C or non-archimedean fields) where “closure” is a dangerous operation. It’s also what one does in practice when actually computing a blow-up (at least for me).
March 16, 2011 at 11:07 am
(The updated blow-up chapter is now posted, see https://math216.wordpress.com/2011/03/16/blowing-up/ , but is not substantively different from the version Brian was responding to.) I still find that the computations are equally accessible (and equally inaccessible) by computing things by embedding them in something smooth (via by the blow-up closure lemma). In particular, I think all of the exercises in the (revised) last section are gettable. I could imagine that this functorial definition for affines is very useful, but as it isn’t directly necessary for anything that will be done later in the notes, to keep the notes from further ballooning, I’ve tentatively not made more additions.
I’m not sure whether this can be made into a mathematical statement, but I find that blow-ups are computationally hard, in the same sense that taking closures are, and computing normalizations. (The blow-up closure lemma at least provides an explicit connection between taking closures and blowing up.) I don’t think I’m missing some clever trick to make them accessible, but it’s important to have enough practice that you can actually compute things. (This last paragraph is intended not for Brian, but for the wider world.)
March 18, 2011 at 1:13 am
Dear Ravi, in (20.1) the sentence should begin, I think, with “If $f:X \rightarrow Y is an affine morphism…” rather than “If $f:X \hookrightarrow Y is an affine morphism…”, since I guess you don’t want to state isomorphy of cohomology only for closed immersions.
By the way, this is the friendliest introduction to cohomology I have ever seen!
Best wishes,
Georges.
March 18, 2011 at 2:43 pm
Dear Georges,
Thanks for both comments! The first is now fixed (in the next version).
best,
Ravi
March 18, 2011 at 1:21 am
On a different note, I had always wondered how I look in other people’s eyes. Now, thanks to your avatar of me, I know 🙂
March 18, 2011 at 2:44 pm
I wish I could take credit for it! 🙂
April 10, 2011 at 2:00 pm
In the universal property that you describe for relative Proj it is unclear where O(1) comes in. I found some old class-notes of yours online which do this part better I think: math.stanford.edu/~vakil/0506-216/216class24.ps
April 17, 2011 at 11:10 am
Thanks! I’m going to rethink some of that exposition, and I’ll keep this in mind. (My intended rethinking wasn’t originally going to address this; Brian Conrad, and later exposition, made me realize that it is easier to not restrict to finitely generated algebras in the definition, and instead restrict only when that hypothesis is needed for a theorem.) If you can say a couple of words on what in the 05-06 notes helped (that was lost later), I could try to keep it in. (And if anyone else was particularly confused on this point, please let me know too… I find this one of the confusing things. I continue to be surprised that graded rings are much harder for me than general machinery.)
April 18, 2011 at 3:39 pm
Sorry I was so obscure about this. The main advantage of the class notes is simply that you are explicit that S_1 = O(1). Also, postponing the issue of when two sheaf maps alpha induce the same scheme morphism made the course notes feel more clear, even if in reality they were less precise!
May 16, 2011 at 11:22 am
Yes, I was confused on this point, and the old class notes does help clarify things, in particular what O(1) is. Also, in the current notes it is not explicit that alpha is a map of graded O_X-algebras, as is supposed to be analogous to the triangular diagram in the definition of relative Spec I believe. Another omission is the “canonical isomorphism L \cong f^*O(1)”; I am not sure about the significance of this and if it is already somewhere in the current definition. For me another good thing in the old notes is that they use the existence of a unique arrow when describing the universal property, which is more akin to how fiber products and normalizations are introduced earlier.
Also a tiny issue: as here the definition is closely related to exercise 17.4.A, I guess it might be clearer if the usage of “f” is consistent in the two places. Lastly, this globalization procedure makes me wonder if we could define something that locally looks like a Proj S. (S. a graded ring), analogous to defining a scheme as locally a Spec A. I guess the relative version of such a thing might be the sheaf Proj we have here. I’m just curious about the non-relative version of the sheaf Proj (and the non-relative version of the sheaf Spec, maybe schemes?). Thank you.
September 2, 2011 at 10:55 am
Hi Yifei,
I’ve flagged (below) your comment as something that I want to think through in detail (along with Ed’s and Pieter’s, see below). I agree with the points that you make. I agree that the usage of “f” should be consistent, and intend to do that at the same time. About the things that look locally like Proj: I’m not sure exactly what you mean. Because anything that looks locally like Proj S. must also look locally like Spec A’s, as Proj S. is covered by Spec’s, so you would again obtain the category of schemes.
September 19, 2011 at 8:10 am
Thank you for your response. For the last point, yes, we would again obtain the category of schemes, by 5.5.7 or more generally 8.3.J in the September 6, 2011 version of the notes.
April 18, 2011 at 7:33 pm
Or rather, O(1) is the pullback of S_1. (This is not what was confusing, but may still be taken as evidence that I was confused by something.)
April 21, 2011 at 7:03 am
Thanks! That’s now “in the system”, and I’ll think this through at some point.
June 9, 2011 at 9:57 pm
On relative Proj: I was also confused by the role of \O(1) at first.
I haven’t thought this through in detail, but it seems you could describe \mathcal{P}roj as an adjoint functor. On the one hand, we have a category whose objects are pairs (pi,L), where pi:Y -> X is a scheme over X and L is a quasicoherent sheaf on Y, and where morphisms (pi,L) -> (pi’,L’) are morphisms of schemes f:Y -> Y’ over X such that f^*L’ = L (or maybe we should replace equality by isomorphism, and make this isomorphism part of the data?). The other category is the category of quasicoherent sheaves of graded O_X algebras on X satisfying the hypotheses of 18.2.1, with the necessary equivalence relation on morphisms.
Then we have a functor from the first category to the second sending (pi,L) to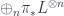 , and a functor in the opposite direction sending S to (\beta:\mathcal{P}roj S -> X, \O(1)), and we want this to be the right adjoint to the first functor.
, and a functor in the opposite direction sending S to (\beta:\mathcal{P}roj S -> X, \O(1)), and we want this to be the right adjoint to the first functor.
There may be some hypotheses missing in what I’ve described above, but if this could be made to work, I would regard this as a better description. I realise some people may prefer a more concrete description, but I find that I’m more likely to take a definition or construction seriously if it’s presented in a more categorical way.
Some minor corrections: Proj needs to be made curly in the last two paragraphs before ex 18.2.A, as does L.
September 2, 2011 at 10:51 am
Thanks! I’ve made the minor corrections. I’ve not yet thought through the main part of your comment… philosophically I’m very much in agreement, and I’ll need to take some thinking it through, as I remember contorting myself into knots with the right definition of Proj.
September 4, 2011 at 9:06 am
I’ve realised that there may be some problems with my suggestion. Namely, what does the proposed right adjoint do to morphisms? For example, if X = Spec A is affine and are graded
are graded 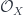 algebras corresponding to graded A-algebras S and S’, then a morphism
algebras corresponding to graded A-algebras S and S’, then a morphism  need not give a morphism Proj S’
need not give a morphism Proj S’ 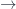 Proj S.
Proj S.
September 4, 2011 at 1:07 pm
You may be able to fix this by restricting to finite morphisms.
September 7, 2011 at 11:30 am
Just to make sure I understand you correctly, do you mean restrict the morphisms in the category of schemes over X with q.c. sheaves to finite morphisms, and restrict the morphisms in the category of graded -algebras to morphisms which on open affines are finite morphisms of algebras?
-algebras to morphisms which on open affines are finite morphisms of algebras?
March 25, 2012 at 5:44 pm
Late response: I’ve currently given in, and defined relative Proj by construction and not by universal property, see here.
July 19, 2011 at 1:49 pm
I’d asked if anyone solved 20.2.E for them to email me. (Note: the exercise remains 20.2.E even in the version current as of today = July 19, 2011) Yifei Zhu did, with a nice solution, and a natural question: if is a quasicompact separated morphism, and
is a quasicompact separated morphism, and 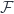 is a quasicoherent sheaf on
is a quasicoherent sheaf on  , for
, for  , must
, must  be an isomorphism? I’ve added to the notes an example showing that it needn’t be: consider
be an isomorphism? I’ve added to the notes an example showing that it needn’t be: consider  ,
,  ,
, 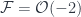 , and let
, and let 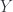 be a point
be a point 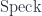 .
.
Is there an easy example showing that it needn’t be injective? I spent 60 seconds thinking of an example where is affine, but
is affine, but 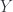 isn’t, with some
isn’t, with some 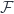 whose pushforward is easily seen to have some higher cohomology, but didn’t succeed.
whose pushforward is easily seen to have some higher cohomology, but didn’t succeed.
September 7, 2011 at 7:42 am
Leray says that the simplest example f:X —> Y of the type you want will involve a non-zero H^2 on Y, a non-zero R^1 f_*, and a non-zero differential. So the obvious guess (to me) is: X = (A^2 – {0}) x A^1, and Y = A^3 – {0}, and the map (x,y,z) —> (x,y,z), i.e., remove {0} x G_m. This is an open immersion with complement of codimension 2, so f_* O_X = O_Y. Moreover, one can compute easily enough (say by Cech) that H^2(Y,O_Y) is non-zero, while H^2(X,O_X) is 0, so we win. If you want an example with affine X, you need f to be non-separated….
September 8, 2011 at 1:02 pm
That’s a very clear example — excellent by all possible metrics. Thanks! How/why did you say that for an example with affine X, f needs to be non-separated?
September 8, 2011 at 2:30 pm
Oops, sorry, I misspoke! I meant that if you want an example with X affine, then Y must be non-separated: if X is affine and Y is separated (over Spec(Z), or any base over which X is affine), then any map X —> Y is affine, so H^i(Y,f_* (F)) =~ H^i(X,F).
September 8, 2011 at 2:37 pm
Ah yes, that’s great, thanks!
March 25, 2012 at 5:43 pm
About relative Proj: I’ve caved in, and gone back to a definition by construction, rather than by universal property. I refer to the stacks project for a universal property. This seems to be one of those rare cases where the universal property makes life worse, not better. But feel dirty.
I’ll discuss this a bit more in the 21th posting, which will come soon (hopefully in the next week).